高斯滤波器是一种线性滤波器，可以有明显效果地的抑制噪声，平滑图像。其作用原理和均值滤波器类似，都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数都是相同的为1;而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小。所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小。

  既然名称为高斯滤波器，那么其和高斯分布(正态分布)是有一定的关系的。一个二维的高斯函数如下：

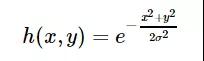
  其中(x,y)(x,y)为点坐标，在图像处理中可认为是整数;σσ是标准差。要想得到一个高斯滤波器的模板，可以对高斯函数进行离散化，得到的高斯函数值作为模板的系数。例如：要产生一个3×33×3的高斯滤波器模板，以模板的中心位置为坐标原点进行采样。模板在各个位置的坐标，如下所示(x轴水平向右，y轴竖直向下)

  对于窗口模板的大小为(2k+1)×(2k+1)，模板中各个元素值的计算公式如下：

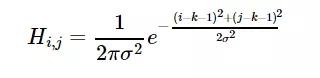
  整数形式的，则有必要进行归一化处理，将模板左上角的值归一化为1，下面会具体介绍。使用整数的模板时，需要在模板的前面加一个系数，系数为也就是模板系数和的倒数。

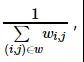
  需要一个二维数组，存放生成的系数(这里假设模板的最大尺寸不会超过11);第二个参数是模板的大小(别超过11);第三个参数就较为重要了，是高斯分布的标准差。

  生成的过程，首先是根据模板的大小，找到模板的中心位置ksize/2。然后就是遍历，根据高斯分布的函数，计算模板中每个系数的值。

  需要注意的是，最后归一化的过程，使用模板左上角的系数的倒数作为归一化的系数(左上角的系数值被归一化为1)，模板中的每个系数都乘以该值(左上角系数的倒数)，然后将得到的值取整，就得到了整数型的高斯滤波器模板。

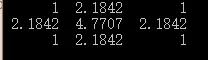
  至于小数形式的生成也最简单，去掉归一化的过程，并且在求解过程后，模板的每个系数要除以所有系数的和。具体代码如下：

  通过上述的实现过程，显而易见，高斯滤波器模板的生成最重要的参数就是高斯分布的标准差σσ。标准差代表着数据的离散程度，如果σσ较小，那么生成的模板的中心系数较大，而周围的系数较小，这样对图像的平滑效果就不是很明显;反之，σσ较大，则生成的模板的各个系数相差就不是很大，比较类似均值模板，对图像的平滑效果比较明显。

  横轴表示可能得取值x，竖轴表示概率分布密度F(x)，那么不难理解这样一个曲线与x轴围成的图形面积为1。σσ(标准差)决定了这个图形的宽度，能得出这样的结论：σσ越大，则图形越宽，尖峰越小，图形较为平缓;σσ越小，则图形越窄，越集中，中间部分也就越尖，图形变化比较剧烈。这其实很好理解，如果sigma也就是标准差越大，则表示该密度分布一定比较分散，由于面积为1，于是尖峰部分减小，宽度越宽(分布越分散);同理，当σσ越小时，说明密度分布较为集中，于是尖峰越尖，宽度越窄!

  σσ越大，分布越分散，各部分比重差别不大，于是生成的模板各元素值差别不大，类似于平均模板；

  σσ越小，分布越集中，中间部分所占比重远高于别的部分，反映到高斯模板上就是中心元素值远大于其他元素值，于是自然而然就等于中间值得点运算。

  在生成高斯模板好，其简单的实现和其他的空间滤波器没有区别，具体代码如下：

  只处理单通道或者三通道图像，模板生成后，其滤波(卷积过程)就最简单了。不过，这样的高斯滤波过程，其循环运算次数为m×n×ksize2，其中m，n为图像的尺寸;ksize为高斯滤波器的尺寸。这样其时间复杂度为O(ksize2)，随滤波器的模板的尺寸呈平方增长，当高斯滤波器的尺寸较大时，其运算效率是极低的。为了，提高滤波的运算速度，可以将二维的高斯滤波过程分解开来。

  由于高斯函数的可分离性，尺寸较大的高斯滤波器可以分成两步进行：首先将图像在水平(竖直)方向与一维高斯函数进行卷积;然后将卷积后的结果在竖直(水平)方向使用相同的一维高斯函数得到的模板进行卷积运算。具体实现代码如下：

  代码没有重构较长，不过其实现原理是最简单的。首先得到一维高斯函数的模板，在卷积(滤波)的过程中，保持行不变，列变化，在水平方向上做卷积运算;接着在上述得到的结果上，保持列不边，行变化，在竖直方向上做卷积运算。这样分解开来，算法的时间复杂度为O(ksize)O(ksize)，运算量和滤波器的模板尺寸呈线性增长。

  在OpenCV也有对高斯滤波器的封装GaussianBlur，其声明如下：

  二维高斯函数的标准差在x和y方向上应该分别有一个标准差，在上面的代码中一直设其在x和y方向的标准是相等的，在OpenCV中的高斯滤波器中，可以在x和y方向上设置不一样的标准差。

  下图是自己实现的高斯滤波器和OpenCV中的GaussianBlur的结果对比

  上图是5×5,σ=0.8的高斯滤波器，能够准确的看出两个实现得到的结果没有很大的区别。

  高斯滤波器是一种线性平滑滤波器，其滤波器的模板是对二维高斯函数离散得到。由于高斯模板的中心值最大，四周逐渐减小，其滤波后的结果相对于均值滤波器来说更好。

  高斯滤波器最重要的参数就是高斯分布的标准差σσ，标准差和高斯滤波器的平滑能力有很大的能力，σσ越大，高斯滤波器的频带就较宽，对图像的平滑程度就越好。通过调节σσ参数，可以平衡对图像的噪声的抑制和对图像的模糊。